Орієнт ація, узагальнення поняття направлення на прямий на геометричній фігурі більш складної структури.

Орієнтація на прямій. Точка може рухатися по прямій в двох протилежних напрямках. Наприклад, по горизонтальній прямій АВ (рис. 1) можливо або рух справа наліво, або рух зліва направо. Пряма разом із зазначенням певного напрямку на ній називається орієнтованої прямий.

Орієнтація на кривій. Аналогічно орієнтації на прямий кожну замкнуту криву можна орієнтувати або проти годинникової стрілки (рис. 2), або за годинниковою стрілкою (рис. 3).

Орієнтація на площині. Нехай будь-якої шматок площині обмежений простий замкнутої кривої (т. Е. Замкнутій кривій без кратних точок). Цю криву можна орієнтувати двома рівними способами. При орієнтації кривої орієнтується і обмежений нею шматок площині. Дві прості замкнуті криві на площині вважаються орієнтованими однаково, якщо при обході цих кривих за вказаним напрямом обмежені ними шматки площині залишаються з однієї і тієї ж сторони (в обох випадках або праворуч, або ліворуч). Наприклад, на рис. 2 і 4 криві орієнтовані однаково, а крива на рис. 3 - протилежно першим двом. Досить вибрати на площині О. однієї простої замкнутої кривої, щоб тим самим визначилася відповідна О. всіх інших таких кривих, що лежать на тій же площині. Площина разом з певним вибором О. лежать на ній простих замкнутих кривих називаються орієнтованої площиною. Кожна площину може бути орієнтована двома способами. О. площині може бути також задана за допомогою вибору системи декартових координат. Якщо на площині обрані осі координат Ох і Оу з певними позитивними напрямами на них, то цього вибору відповідає О. площині, при якій коло з центром на початку координат орієнтована в напрямку від позитивного напрямку осі Ox до позитивного напрямку осі Оу. Наприклад, системи координат на рис. 5 і 6 визначають одну і ту ж О. площині. Система ж координат на рис. 7 орієнтована протилежним чином.

Координати (x, у) і (х ', у') в двох прямолінійних системах координат на площині пов'язані співвідношеннями

х '= a11x + a12y + b1

y '= a21x + a22y + b2,

де визначник

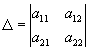
відмінний від нуля. Системи координат (х, у) і (х ', у') орієнтовані однаково, якщо D> 0, і протилежно, якщо D <0. Цю обставину можна використовувати для суворої аналітичної теорії О. на площині. Легко бачити, що безліч S всіх прямолінійних систем координат розпадається на два підмножини S 'і S' 'так, що в межах S' (і в межах S '') всі системи координат пов'язані перетвореннями з D> 0, а будь-яка система координат з S 'пов'язана з системою координат з S' 'перетворенням з D <0. Вибрати О. площині - це і означає вибрати одне з множин S 'або S ". Вибір О. на площині визначає знак розташованих на площині кутів і площ, обмежених орієнтованими замкнутими кривими. Наприклад, формула

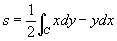
площі s, обмеженій замкненій кривій с, орієнтованої в напрямку стрілки, в разі правої системи координат (рис. 5 і 6) приведе до позитивної площі для фігур рис. 2 і 4 і до негативної - для фігури на рис. 3. Навпаки, в лівій системі координат (рис. 7) обчислені за формулою площі s фігури на рис. 3 будуть позитивні, площі самих фігур на рис. 2 і 4 - негативні.

Орієнтація поверхні. Подібно до того, як була вище визначена О. площині, може бути визначена О. будь-якій поверхні, що ділить простір на дві частини (наприклад, сфери). Для цього розглядаються шматки поверхні, обмежені простими замкнутими лініями. Орієнтувати такий шматок поверхні - це значить вибрати певну О. обмежує його кривої. Два шматка поверхні називаються орієнтованими однаково, якщо при обході обмежують ці шматки поверхні кривих в зазначеному напрямку самі шматки поверхні залишаються з однієї і тієї ж сторони. Наприклад, поверхні на рис. 8 і 9 двох кубів орієнтовані однаково, а поверхня третього (рис. 10) - протилежним чином. Поверхня разом з певною О. шматків, обмежених простими замкнутими кривими, і називають орієнтованої поверхнею. Не всяка поверхня може бути орієнтована (див. орієнтована поверхню ). Однак поверхні, що обмежують частину простору, завжди належать до числа орієнтується.

Орієнтація простору. Нехай замкнута поверхня обмежує певний шматок простору. Кажуть, що така поверхня орієнтована правим чином, якщо шматки цієї поверхні, що спостерігаються зовні, представляються орієнтованими проти годинникової стрілки, подібно кубів на рис. 8 і 9. Навпаки, О. замкнутої поверхні, що обмежує шматок простору, вважається лівою, якщо її шматки орієнтовані при спостереженні зовні за годинниковою стрілкою, подібно кубу на рис. 10. Вибір певної О. замкнутих поверхонь без самоперетинів називається О. самого тривимірного простору. Т. о., Існують дві О. тривимірного простору: права і ліва. О. простору можна встановити також за допомогою вибору системи декартових координат. Якщо обрані осі координат Ox, Оу і Oz з певними позитивними напрямами на них, то відповідна О. простору визначається наступною умовою: розглядається будь-якої тетраедр ОАВС з вершиною О в початку і вершинами А, В, С відповідно на позитивних променях осей Ox, Оу і Oz (рис. 11, 12), трикутник АВС, що лежить на поверхні цього тетраедра, орієнтується в порядку АВС (т. е. від осі Ox до осі Оу і потім до осі Oz); цим визначається О. поверхні тетраедра, а отже, і всього простору. Вибір осей на рис. 11 відповідає правій О. простору, вибір же осей на рис. 12 - лівої О. простору. За вказаним принципом самі системи координат в просторі поділяються на праві і ліві. Від вибору О. простору залежить знак обсягів, обмежених орієнтованими поверхнями, сенс векторного твору двох векторів і т.п.

У науковій та навчальній літературі вживаються як ліва, так і права системи просторових координат. Наприклад, у вітчизняних творах з математики поширене вживання лівої системи, в творах же з механіки і фізики - правої системи.

Поняття «О.» поширюється також і на багатовимірні простору .

Мал. до ст. Орієнтація.